【数学】二次関数が簡単になる解き方とグラフの書き方

「二次関数あたりから数学が嫌いになった」という人は少なくないと思います。
二次関数は文字がたくさん出てきて、二乗があり、グラフまで描かされます。

苦手になるのに十分な要素があります。

しかし、二次関数を嫌う人でも、「一次関数は簡単だった」と感じているはずです。
ならば、一次から二次へと、たった1つしか増えていないので、それほど難しくなるはずがありません。

二次関数は難しくありません。

ではなぜ、二次関数を難しいと感じてしまうのでしょうか。
それは、「二次関数は難しいはずだ」という先入観があるからです。

この記事を読んでいただければ、「え、二次関数ってたったそれだけのことなの」と思っていただけるはずです。

二次関数は一次関数から「1つ増えただけ」

二次関数嫌いの先入観を解消するには、「二次関数は一次関数から1つ増えただけ」と思うことが大切です。

一次関数を発展させたのが二次関数です。

一次関数は、例えば「y=ax」です。
aに「2」を入れれば「y=2x」になります。

これが簡単なのは、「yはxの2倍」とすぐに理解できるからです。

「yはxの2倍」なら、

と、九九の2の段のようにスラスラでてきます。

そのため、一次関数を難しいと感じる人はほとんどいません。

二次関数も、一次関数を解くのと同じ感覚で解いていけばいいのです。

二次関数は、例えば「y=ax²」と表記します。
aに「2」を入れれば「y=2x²」になります。

これは、「yはxの二乗の2倍」にすぎません。

先ほどの「y=2x」の「x」が「xの二乗」に変わっただけです。
二乗は「同じ数を掛ける」だけなので、難しくありません。

「yはxの二乗の2倍」ならこうすればよいわけです。

二次関数は便利

数学を嫌いになる人は「日常生活で使わないから、苦労して覚える気持ちになれない」と思っているのではないでしょうか。

例えば英語を覚えれば、洋楽ロックの歌詞の意味を理解できたり、アメリカ人と話すことができたりします。

国語を覚えれば、本を読んだり、美しい文章を書いたりすることができます。

しかし数学を覚えても、何の得もないような気がします。

ところが、そうではないのです。

特に二次関数はとても使い勝手がよい数学の知識です。

縦が長くなると横も長くなる面積を求めることができる

二次関数の利用方法を考えてみましょう。

あるパネルメーカーが、長方形のパネルをつくっているとします。

このメーカーは、パネルの大きさを「横の長さを縦の長さの2倍にする」と決めていたとします。

例えば、縦2メートルなら、横は2倍の4メートルになります。

この長方形のパネルを床に貼っていくとき、10枚で何平方メートルになるでしょうか。

パネル1枚の面積は8平方メートルです。
「2メートル×4メートル」を計算すれば出ます。

これが10枚なので、面積は80平方メートルです。
「10枚×8平方メートル」を計算するだけで出ます。

では、パネルを変えて、縦3メートルとします。
横の長さは縦の2倍なので、6メートルになります。

この3×6メートルのパネルを床に貼っていったら、何枚で何平方メートルになるでしょうか。

答えは180平方メートルです。

では縦9メートル、横18メートルのパネルなら、何枚で何平方センチメートルになるでしょうか。
縦44メートル、横88メートルのパネルならいかがでしょうか。

これらをいちいち計算するのは、とても面倒です。

この4枚のパネルを並べてみましょう。

「縦×2＝横」という関係になっています。

そこで縦をxとして、面積をyとすると、次のような計算式をつくることができます。

y＝2x²という二次関数の式ができました。

さらに、タイルの枚数をnとしてみましょう。

タイル1枚の面積が「2x²」なので、タイルn枚の面積は「2nx²」になります。

ここまで準備できると、例えば「縦38メートルのタイルを25枚並べたときの面積は何平方メートルになるか」という質問の答えを簡単に出すことができます。

なので、縦＝x＝38、タイル枚数＝n＝25を入れ、y＝2×25×（38）²を解くだけです。

答えは72,200平方メートルになります。

二次関数の性質があるものを、二次関数の数式で表すと一瞬で答えが出ます。
二次関数はこれほど便利な計算式なのです。

「マイナス」を二乗すると「プラス」になる

続いて、二次関数のグラフを書いていきましょう。

二次関数のグラフも、多くの生徒から嫌われています。
それは二次関数のグラフの形が「変な曲線」であり「上から下へ、下から上へと動く」からです。

一次関数のグラフはとても単純でした。
直線が、斜めに走っているだけです。

そのため、二次関数のグラフは、一次関数のグラフとはまるで別物のように感じる人も少なくありません。

しかしグラフも「二次関数は一次関数から1つ増えただけ」です。
一次関数の発展形が二次関数です。

まずは一次関数のグラフを描いてみよう

例えば、一次関数「y=2x」は、次のようなグラフになります。

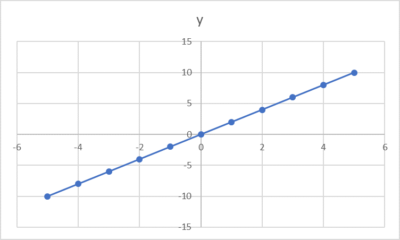
このグラフをつくっている数字は以下のとおりです。

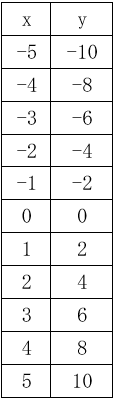
xの数字を「y=2x」に入れていけばyの値が出て、「xとy」の組み合わせをグラフに落としていけば、上記の右肩上がりの直線ができあがります。

一次関数のグラフを描くように二次関数のグラフを描く

二次関数のグラフを描くときも、一次関数のグラフと同じ要領で描いていきます。

例えば、y=2x²のグラフはこのようになります。

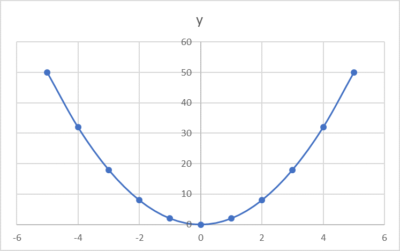
このグラフをつくっているデータは以下のとおりです。

xの数字を「y=2x²」に入れていけば、yの値が出て、「xとy」の組み合わせをグラフに落としていけば、「下方向のとんがり曲線」ができます。

ここまでの説明を読んで「一次関数のグラフの形と二次関数のグラフの形は、似ても似つかないではないか」と思った人もいるでしょう。

一次関数のグラフは左下から右上へ、一直線に伸びています。

二次関数のグラフは左上から曲がりながら落ちてきて、右上に向かって曲がりながら登っています。

確かに、性質は全然違います。

しかし、それでもなお、この2つのグラフは、とてもよく似ているのです。

グニャリと曲げるのは二乗

「y=2x」（直線）と「y=2x²」（曲線）の2つのグラフ並べて「直線をグニャリと曲げただけ」と思いながら見てください。

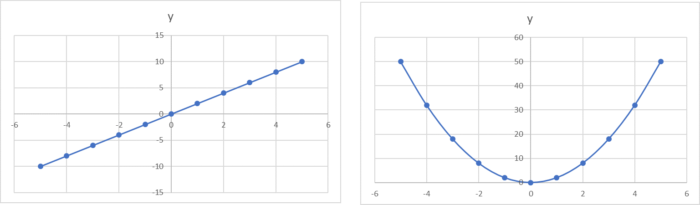
いかがでしょうか。

「直線をグニャリと曲げただけ」と思って見続けると、不思議とそのように見えてきますよね。

では、直線をどのようにしてグニャリと曲げたのでしょうか。

曲げる力は、二次関数が持っています。

直線は一次関数で「y=2x」でした。グニャリと曲がった曲線は二次関数で「y=2x²」でした。
「x」を「x²」にするだけで、グニャリと曲がるのです。

ではなぜ「x²」にはグニャリと曲げる力があるのでしょうか。

まず、xにxを掛けているので、xの数字を増やすと、かなりのスピードでx²増えていきます。

「1、2、3、4」をそれぞれ2倍にするだけなら「2、4、6、8」と増えていくだけですが、「1、2、3、4」をそれぞれ二乗にすると「1、4、9、16」と急増していきます。

そして二乗には、もうひとつ重要な性質があります。
それは「マイナスを二乗するとプラスになる」という性質です。

「－2×－2」は「プラス4」になり、「2×2」と同じ数字になってしまうのです。

そのため、xのマイナスの領域では、xのプラスの領域と同じように上昇していくのです。

グラフにすると「数字が見える」

二次関数を嫌う人はたくさんいます。
それは、二次関数の勉強では、グラフをたくさん描かされるからでしょう。
数字を追うだけでも大変なのに、その上、曲線を描かされるので嫌になってしまうのは当然です。

しかしこう考えてみてはいかがでしょうか。

数字を並べただけではみえないのに、グラフにした途端にみえてくるのです。

下の数字は、とてもつまらないものです。
数字が並んでいるだけで無味乾燥です。
数字に意味があるように思えません。

では数式ならどうでしょうか。

上の数字は、この数式から算出しています。

数式でも、さらに何を伝えようとしているのかわかりません。

ところが、この数式を使って上記の数字を導き出し、それをグラフにするとこのようになります。

この曲線は「グワーンと下降して、ギューンと上昇」しています。

もしくは、「マイナスの領域に進めば進むほど上昇し、プラスの領域に進んでも上昇する」という性質もわかります。

あの無味乾燥の数字の集まりには、このような「意味のある」形が含まれていたのです。

数字の集まりのなかから意味をみつけるには、グラフにするのが最も効果的です。

まとめ～二次関数を乗り切れば数学は「なんとかなる」

二次関数を苦手に感じるのは「気のせいだった」ことが理解できたのではないでしょうか。
実は、数学を嫌っている人の多くは、気のせいで数学を苦手にしています。

では、どのように気のせいを失くしていったらよいのでしょうか。

それは、数学の便利さを感じることです。
数学は、自然現象のなかに埋もれていてみえにくくなっている法則を、みえやすくするための技術です。

数学は便利グッズです。

二次関数のグラフは、便利グッズの最たるものです。
意味のない数字の集まりに「グワーンと下降して、ギューンと上昇」する線が隠されていることが、グラフにすることでわかります。

二次関数を乗り越えることができると、数学が便利グッズであることがわかるので、数学が好きになるかもしれません。

以下の記事もあわせて読んでみよう！

中学の数学【平方根】を理解して受験を乗り切ろう！

高校受験の際に大きな壁となる平方根。あなたはしっかりと理解できていますか。本記事をご覧の皆さんは平方根が苦手な生徒さん達でしょう。「ルートっ…

数学【二次方程式】の解き方が分かれば強い味方にできる！

三年生で学ぶ二次方程式には三年間で学んだことがすべて詰まっています。中学生の時に学ぶ解き方は三種類。問題を解くことだけを考えると簡単なように…

三平方の定理・公式を簡単に覚える方法【中学数学】

数学の知識のなかには、これさえ乗り切ればあとはいくらでも応用がきく、というものがあります。 そのひとつが三平方の定理です。 三平方の定理…

この記事を監修した人

チーム個別指導塾
「大成会」代表
池端 祐次

2013年「合同会社大成会」を設立し、代表を務める。学習塾の運営、教育コンサルティングを主な事業内容とし、札幌市区のチーム個別指導塾「大成会」を運営する。「完璧にできなくても、ただ成りたいものに成れるだけの勉強はできて欲しい。」をモットーに、これまで数多くの生徒さんを志望校の合格へと導いてきた。

FacebookはこちらからLINE＠友だち登録