
数学の知識のなかには、これさえ乗り切ればあとはいくらでも応用がきく、というものがあります。
そのひとつが三平方の定理です。
三平方の定理は中学校で習う内容ですが、これをしっかり理解しておくと、高校の数学の授業が面白いように頭のなかに入ってきます。
ただ、中学生には、三平方の定理は難しく感じるはずです。
そこで、三平方の定理と、そこで使われる公式を、簡単にかつ楽しく覚える方法を紹介します。
三平方の定理の内容はマジックのようです。
「へえ、不思議、面白い」と感じるはずです。
直角三角形は不思議
三平方の定理とは、「不思議な直角三角形」の不思議さを説明したものです。
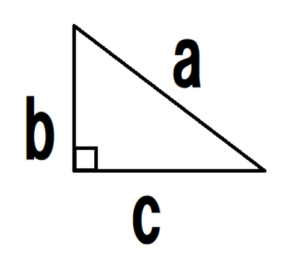
直角三角形は、上の図のような形をしていて、内側の3つの角のうち、1つが90度になっています。
90度(直角)を挟む辺の長さをb、cとして、斜辺をaとすると、次の関係が成り立ちます。
a2は「aの二乗」といい、「a×a=a2」と表記します。
a2=b2+c2の関係が成り立つのは、直角三角形だけです。
これだけでも不思議ですが、さらに不思議なことがあります。
それは「a=b+c」にも「a3=b3+c3」にもならないことです。
3つの辺の長さを二乗しないと「調和」が取れないのです。
そうなると「三角形」と「直角」という2つの性質が合体したときにだけ、なぜ「3つの辺の二乗がa2=b2+c2の関係になる」のか、という疑問がわきます。
この不思議な関係は、説明できます。
そしてその説明を聞けば、不思議な現象はもう不思議でなくなります。
大きい正方形と小さい正方形で解く
それでは、「直角三角形のa2=b2+c2は不思議ではなく、当たり前の現象である」ことを説明します。
下の図をみてください。
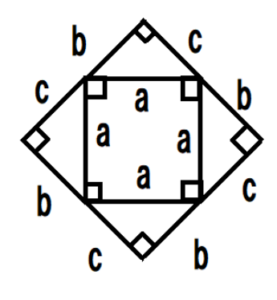
一辺が「b+C」の正方形のなかに、一辺が「a」の正方形が入っています。
これを分解すると、下の図ようになります。
ここがとても重要なので上の図が下の図のように分解できることが「見えてくる」まで、2つの図をじっと見つめてみてください。
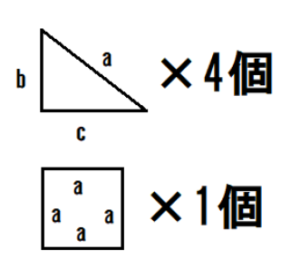
さらに上の図は、下の図のようになります。
これは理解しやすいでしょう。
上の図の面積を求めてみましょう。
計算式で表すと、次のようになります。
この計算式をA式と呼びます。
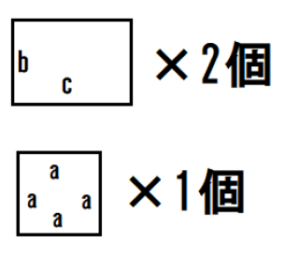
さて、上の図は、元々は下の図でした。

上の図の面積を計算式で表すと、次のようになります。
この計算式をB式と呼びます。
このB式は、先ほどのA式と同じ面積を求めているので「A=B」となり、次のような計算式が成り立ちます。
これを展開していきましょう。
さらに展開すると、以下のようになります。
したがって、直角三角形の3つの辺の長さが以下のようになっているとき、a2=b2+c2が成り立つのです。
これが三平方の定理です。

まだある「直角三角形の不思議」
直角三角形の不思議な現象は、実は全然不思議ではなく、大きな正方形と小さな正方形の面積を求めることで、簡単に説明できることがわかりました。
しかし、安心することはできません。
なぜなら、直角三角形には「別の不思議現象」があるからです。
せっかく三平方の定理をきっかけにして直角三角形の世界に入ったので、もう少し奥に進んでみましょう。
直角三角形にはなんと、以下のようなものが存在するのです。
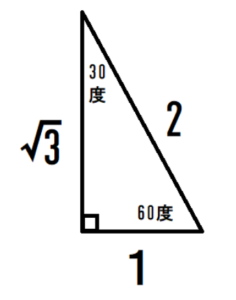
直角三角形の直角(90度)以外の2つの角度が30度と60度の場合のみ、1、2、3がそろってしまうのです。
数字として、とても「美しい」現象になっています。
√とは「二乗すると、なかの数字になる」という意味の記号です。
つまりは、√3は、「√3×√3」で3になります。
それで、三平方の定理を使えば、
になることは納得できます。
そのため、次の内容は正しいことになります。
このことは三平方の定理から導くことができますが、では3つの辺のうち、「1」の長さが2倍になって「2」に変わったら、この関係はどうなるのでしょうか。
つまり、次のことは正しいといえるのでしょうか。
以下の図のようになるのでしょうか。
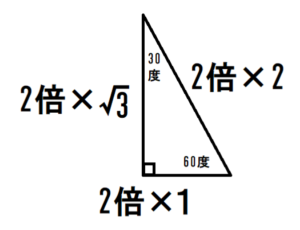
先に結論を紹介すると「なります」。
なぜなら三平方の定理から次のことが成立するからです。
これを展開すると、このようになります。
では2倍ではなく、何倍になっても「1、2、√3」の比は成立するのでしょうか。
例えば、1がN倍になっても「N倍×1、N倍×2、N倍×√3」となるのでしょうか。
答えは「なります」。
それを説明していきます。
下の図をみてください。
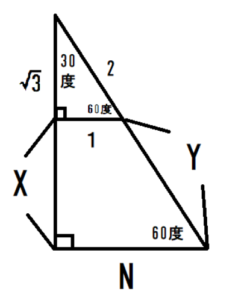
大きな直角三角形のなかに、小さな直角三角形が入っています。
小さな直角三角形は「1、2、√3」です。
大きな直角三角形は「底辺1をN倍にした」ものです。
「Xと√3を足したもの」が「N倍×√3」になり、「2とYを足したもの」が「N倍×2」になれば、底辺1がN倍になっても「N倍×1、N倍×2、N倍×√3」が成立する、といえます。
まず、「Xと√3を足したものがN倍×√3になり、2とYを足したものがN倍×2になれば」を数式にします。
X+√3=√3N …A式(まだ仮定の状態。これが成立するかどうかわからない)
2+Y=2N …B式(まだ仮定。これが成立するかどうかわからない)
上の2つの式は「まだ」正しいかどうかわかりません。
まだ仮定の状態です。
続いて、底辺をNとする、大きな三角形の面積を求めます。
これは三平方の定理から次のように導き出すことができます。
この式が正しいことは、三平方の定理から証明されます。
これで準備は整いました。
不明な文字がX、Y、Nと3つあり、計算式がA式、B式、C式の3つあるので、X、Y、Nを求めることができます。
3つの式を並べてみましょう。
・X+√3=√3N …A式(仮定)
・2+Y=2N …B式(仮定)
・(2+Y)2=(X+√3)2+N2 …C式(三平方の定理)
C式は三平方の定理から「正しい」ことがわかっているので、C式にA式とB式を挿入して、計算式が成立すれば、A式とB式の「仮定」が正しかったことになります。
A式とB式を次のように変えます
・X=√3(N-1)
・Y=2(N-1)
これをC式に入れると、次のようになります。
これは成立します。
実際に解いてみてください。
見事に両辺とも「0」になります。
したがって、次のことは正しいといえます。
つまり「1、2、√3」の比はN倍になっても成立することがわかりました。
3、4、5も!
もうひとつ、直角三角形の不思議を紹介します。
3、4、5という連続した数字でも三平方の定理が成立します。
これを計算すると、両辺とも25になります。
3、4、5をすべて2倍しても三平方の定理が成り立ちます。
これを計算すると、両辺とも100になります。
3、4、5を覚えておくと、マッチ棒を3本用意して、それぞれ長さを3センチ、4センチ、5センチにして三角形をつくると、直角三角形になることがわかります。
「1、2、√3」もきれいでしたが、「3、4、5」もきれいです。
三平方の定理は実生活でも使える
 ここまでの説明で「三平方の定理がわかった! すごい!」と感じることができた方は、このあときっと数学が好きになると思います。
ここまでの説明で「三平方の定理がわかった! すごい!」と感じることができた方は、このあときっと数学が好きになると思います。
数字の不思議な現象に接すると「なぜそうなるのか」と知りたくなるでしょう。
そして、「なぜそうなるのか調べること」こそ、数学の「証明」です。
つまり、なぜそうなるのか知りたくなれば、数学は嫌いな教科から好きな教科に変わります。
しかし、ここまでの説明で「三平方の定理はわかったけど、特別すごいとは思わない」と感じている人もいると思います。
そのような人でも、三平方の定理が実生活で役に立つことを知れば、数学を好きになることができるかもしれません。
三平方の定理を覚えておけば、坂道の距離がわかります。
A点とB点を結ぶ坂道が直線だったとします。
この坂道を地図にすると、A-Bの距離とC-Bの距離が同じになってしまいます。
地図は、上空からみた距離しか表すことができないからです。
しかし、C点とB点の直線距離(地図上の距離)と、A点とB点の高さがわかれば、坂道の長さがわかります。
三平方の定理を使って、次の式を解けばよいのです。
三平方の定理を覚えておけば、「直角三角形」をつくることで、2つの辺の長さがわかれば、3本目の辺の長さを求めることができます。
「2つわかれば3つ目がわかる」ということは「2つ計測すれば3つ目を計測しなくてよい」ことであり、計測の作業が効率化します。
まとめ~美しさと利便性
数学には、美しさと利便性の両方があります。
三平方の定理にも、その両方が備わっています。
数学の美しさを「美しい」と思えると、数学の勉強は苦でなくなります。
しかし生徒のなかには、数学を美しいと思えない人もいるでしょう。
そのような人は、数学の利便性を知ってください。
三平方の定理は、ビルづくりや道路づくりなど、建築や土木の建設現場で多用されています。
三平方の定理が発見されていなかったら、ビルも道路もこれほど正確にできていなかったでしょう。
この利便性は、三平方の定理にだけ存在するのではありません。
数学の公式すべてに、利便性が隠されています。
中学や高校での数学の授業は、「すでにわかっている内容を学ぶ」ことになりますが、元々数学は「なぜこのような結果になるのだろうか」「調べてみよう」という気持ちから生まれました。
自然現象を数字で説明するために、数学がつくられたのです。
「すでにわかっている内容を学ぶ」だけだと退屈に感じるかもしれませんが、そこを乗り越えると、数学を学ぶ意義が急にみえてきます。
この記事を監修した人

「大成会」代表
池端 祐次
2013年「合同会社大成会」を設立し、代表を務める。学習塾の運営、教育コンサルティングを主な事業内容とし、札幌市区のチーム個別指導塾「大成会」を運営する。「完璧にできなくても、ただ成りたいものに成れるだけの勉強はできて欲しい。」をモットーに、これまで数多くの生徒さんを志望校の合格へと導いてきた。
















