
時間をかけて勉強しているのに学力が上がらないときは、「暗算」の力を鍛えて「計算」に強くなるようにしてみてください。
暗算と計算の力は、算数や数学の成績を上げるだけではありません。
国語、英語、理科、社会の成績も、暗算と計算の力に引っ張られる形で上がっていくことがあります。
暗算と計算の勉強に力を入れると、
- 最短距離で正解に到着しようとするマインド
- 粘り強く考える学習態度
が養われるからです。
学力向上に欠かせない「効率化と根気」が身につきます。
この記事では、暗算と計算の基礎知識を紹介したうえで、この2つが学力に与えるよい影響を解説します。
暗算と計算の力は、学力を急上昇させる起爆剤になります。
そもそも暗算とは
暗算のことを「頭のなかで行う計算処理」と理解している人は少なくないと思いますが、この短い言葉だけでは暗算のすべてを説明できません。
暗算の正体を探っていきましょう。
「筆算ではない」「尾加法はしない」
 暗算の特徴のひとつに「筆算ではないこと」があります。
暗算の特徴のひとつに「筆算ではないこと」があります。
筆算とは、鉛筆で紙の上に数字を書きながら計算を進めていく方法です。
筆算には尾加法という特徴があります。
尾加法とは、一桁目(一の位)から順に足していく方法で、多くの人が普通に行なっている方法です。
例えば「67+54」という問題が出されたら、普通はまず、2つの数字の一桁目である「7+4」を計算すると思います。
「7+4」は「11」です。
これをAとします。
次に二桁目の「6(0)+5(0)」に注目して「110」を出します。
これをBとします。
そして最後に「A+B=11+110」を計算して「121」を出します。
数字の後ろ(下位の桁のこと。つまり、尾っぽ)から計算するので、尾加法といいます。
「暗算は筆算ではない」ので、暗算では尾加法は使いません。
これが暗算の重要な要素になります。
では、暗算は、尾加法以外のどのような方法で計算処理を行うのでしょうか。
上位の桁から「大体で」計算していく
暗算では、上位の桁から「大体で」計算していきます。
「67+54」における上位の桁とは「6(×10)」と「5(×10)」です。
暗算をするとき、次のように思考します。
だったら、まずは「60+50」を計算してしまおう。
110だ。
つまり「67+54」の答えは「大体110」だ。
「桁上げ」とは、例えば「7+4=11」のように、一桁どうしの計算をした結果、二桁になる現象のことです。
暗算では、正確な数字を出す前に、大体の数字を先に出します。
計算処理では正確さが求められるのに、なぜ、大体の数字を先に求めるのでしょうか。
それは、正確な数字に近づくためです。
「67+54」の正確な答えは、先ほど計算したとおり「121」でした。
しかし筆算では、最初に一桁目を計算するので、最初に得られる数字は「11」(=7+4)です。
11は、121からかなり離れた数字であることは一目瞭然です。
一方、暗算では、最初に大体の計算をして「110」(=60+50)という数字を得ています。
110は、121にかなり近い数字です。
暗算では、大体の数字に近づいてから、詳しい計算をします。
「110」以降の処理の仕方を見ていきましょう。
暗算で次にすることは、「67と60の関係」と「54と50の関係」のチェックです。
ここでは、次のように考えます。
54は50より「4多い」。
ということは、正解は「110より7多く、さらに4多い」。
7+4は11だから、正解は「110より11多い」つまり「121」だ。
ここまでの暗算の流れを確認しておきます。
【スタート】67+54を計算する
↓
【ステップ1】大体の数字を出すために、最も上位の桁である「60+50」を計算する
↓
【ステップ2】「110」を得る
↓
【ステップ3】正確な数字を出すために「67と60の関係」と「54と50の関係」をチェックする
↓
【ステップ4】正確な数字は「110」より「11多い」ことがわかる
↓
【ゴール】答えは121
なぜ大体の計算をするのか
 なぜ暗算では、大体の計算を先にするのでしょう。
なぜ暗算では、大体の計算を先にするのでしょう。
なぜ上位の桁から計算するのでしょうか。
なぜ下位の桁から、地道に正しい計算を積み重ねていかないのでしょうか。
答えは「安心するため」です。
「67+54」が出題されて、すぐに「まあ大体110だろう」とわかれば、安心することができます。
安心とは「あとは、細かい計算をすれば正答にたどり着く」という確信です。
難易度が高い計算になると、この安心がとても重要になります。
「1338+5604+330」を暗算してみましょう。
この大きな数字を見て、少し不安になりませんか。
これを暗算するとき、まず「1000+5000」を計算します。
「大体6000」という数字を得ることができます。
次に百の桁に注目して「300+600+300」を計算して「大体1200」を得ます。
こうすることで「大体6000+大体1200=大体7200」を早期に得ることができます。
「1338+5604+330」の答えは「7272」なので、かなり近づくことができました。
あとは微調整をするだけです。
「338は300より38多い」「604は600より4多い」「330は300より30多い」ことから「トータルで72多い」ことがわかります。
これに「大体7200」を足せば「7272」を簡単に出すことができます。
暗算で最初に大体の計算をするのは、まずは大体の数字で安心できれば、冷静に細かい数字の調整に取り組むことができるからです。
なぜ筆算では上位の桁から計算しないのか
ではなぜ、筆算では下位の桁から計算するのでしょうか。
なぜ筆算では、先に大体の計算をしないのでしょうか。
それは、大体の計算をする必要がないからです。
筆算では、計算した数字を紙に書いておくことができるので、それなら最初から正確な計算をしたほうが効率的なのです。
筆算では「1338+5604+330」を計算するとき、次のように進めます。
十の桁に注目して「30+00+30」を計算して「60」と紙に書いておく。
百の桁に注目して「300+600+300」を計算して「1200」と紙に書いておく。
千の桁に注目して「1000+5000+0000」を計算して「6000」と紙に書いておく。
紙に書いた4つの数字を足して「7272」を導き出す。
「大体の計算」は暗算では便利な方法ですが、「大体」なので誤答するリスクがあります。
暗算では不安が発生するので、不安解消のために「大体の計算による誤答のリスク」を抱えるメリットがあります。
しかし筆算では、計算処理した数字をすべて紙に書いておけるので不安が生じません。
そうであるならば、「大体の計算」のリスクをおかす必要はなく、地道に正確な計算を積み重ねていったほうが効率的です。
究極の暗算は「聴暗算」
 暗算には「視暗算」と「聴暗算」があります。
暗算には「視暗算」と「聴暗算」があります。
「67+54」という数字を見て、頭のなかで計算処理することを視暗算といいます。
見た(視た)だけで計算を進めます。
「ろくじゅうななたすごじゅうよんは?」と聞いただけで、頭のなかで計算することを聴暗算といいます。
聴くだけで計算を進め、数字は見ません。
視暗算は、筆算に近い暗算です。
そのため、暗算の訓練を受けていないと「67+54」を見たときについ「7+4」から始めてしまいます。
究極の暗算は、聴暗算です。
聴暗算では数字を見ることすらできないので、不安になります。
そこで、まずは安心を得ようと上位の桁から計算していく癖がつきます。
「ろくじゅうななたすごじゅうよんは?」と聞いて、すぐに「ろくじゅうたすごじゅうは、110だから、110に近づけばいいんだな」と思うことができます。
微調整をするときのちょっとしたコツ
 ここで、暗算の小さなテクニックを紹介します。
ここで、暗算の小さなテクニックを紹介します。
先ほど「67+54」を暗算するとき「まず60+50を計算して、次に67と60の関係、54と50の関係をチェックする」方法を紹介しました。
この方法には欠点があります。
それは「67と60の関係、54と50の関係をチェックする」と「7+4」を計算しなければならず、桁上がりが発生することです。
桁上がりは計算を複雑にします。
せっかく「60+50」で「大体110」を得ているのに、「7+4」で「11」を得ると、11は「大体10」なので、「大体110」が「大体120」に変わってしまいます。
そこで、桁上げを発生させない方法が有益になります。
「67+54」を「大体70+大体50」として大体の計算をするのです。
ここでは一の桁を四捨五入しています。
67の一の桁を四捨五入すると70になり、54の一の桁を四捨五入すると50になります。
すると「大体70+大体50=大体120」になり、大体の計算結果がさらに正解に近づくことができます。
そして「67と70の関係=-3」「54と50の関係=+4」を計算して、「トータルで+1」が導き出されます。
「大体120+1」で「121」の正解が得られます。
ここで桁上げは発生していません。
このように「四捨五入」と「マイナス」という小さいテクニックを使うと、暗算がよりスムーズに進みます。
暗算が与える計算への効果
暗算の概要を理解できたところで、暗算が与える計算への効果を考えていきましょう。
算数・数学とは計算方法を多く身につける勉強である
暗算は計算方法の一種にすぎません。
そして計算には、足し算・引き算・掛け算・割り算の四則演算以外にも、さまざまな方法があります。
例えば、二次方程式の解の公式を使えば、二次方程式「ax2+bx+c=0」の計算を短時間で実行できてしまいます。
二次方程式の解の公式はこのようになっています。
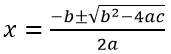
算数・数学の勉強や試験では、とにかく計算をして正解にたどりつく必要があります。
そのとき、暗算でも、四則演算でも、公式でも、何を使ってもかまいません。
つまり、計算ができないことには、算数や数学の成績を上げることはできません。
算数や数学の勉強とは、計算方法を多く身につけることに他なりません。
多くの計算方法を持ち、さらに、短時間で大量の計算処理を行える人が、算数・数学の成績を上げることができます。
暗算ができると計算をワープできる
 暗算は「ワープ」のような効果を持っています。
暗算は「ワープ」のような効果を持っています。
ワープとは、長い距離を一瞬で移動する手段で、SFのなかの技術です。
暗算ができるようなると、面倒な四則演算や複雑な公式を飛ばして、一気に正解まで移動できるようになります。
暗算のワープ効果は、
- 正確な答えを出せる
- 短時間で計算処理を終えることができる
という2つの大きなメリットを生みます。
数学の問題が複雑になると、正解までの計算過程が長くなります。
この計算過程のなかでひとつでも間違えると、ミス以前の計算やミス以後の計算がいくら正しくても正解は出ません。
数学は、ひとつのミスも許されないシビアな世界なのです。
暗算の力は、計算ミスを減らすので、この力を獲得すると正解できる確率を高めることができます。
そして数学の試験は、高度になるほど、レベルが上がるほど、時間との勝負になります。
90分の試験で「2時間あれば全問解けたのに」という言い訳は通用しません。
高度な数学の問題では、計算力以上に思考力が求められるので、思考に時間をかけるには、計算時間を短くするしかありません。
暗算のスキルを身につけると、ある問題の「解き方がわかった」段階で、その問題を終わらせることができます。
暗算ができない人だと、「解き方がわかった」ら、次に「計算をこなす」作業に取り掛からなければなりません。
「数学の力」と「高得点スキル」の違い
 「数学の力」と「数学の試験で高得点を上げるスキル」は似ていますが、別のモノです。
「数学の力」と「数学の試験で高得点を上げるスキル」は似ていますが、別のモノです。
数学の力とは、解く力です。
他の人がまったく解けない数学の問題を、3時間かけて解く人がいますが、この場合「その人には数学の力がある」ということができます。
しかし数学の試験で高得点を取るには、解く力に加えて短い時間で解く力が必要になります。
例えば、AさんとBさんの「数学の力」が同じだったとします。
しかしAさんは、難問を解くのに100分かかります。
Bさんは難問を90分で解きます。
90分の試験でその難問が出たら、Bさんは合格して、Aさんは不合格です。
「数学の力」が同じでも、解く時間に差があれば得点力が異なってきます。
だから、暗算の力が求められるわけです。
暗算と計算の力が身につくと、なぜ英語や国語などの教科の成績も上がるのか
暗算と計算の力を身につけると、国語、英語、社会、理科といった、算数・数学以外の成績も向上します。
そのメカニズムをみていきましょう。
暗算では「最短距離で正解に到着しようとするマインド」と「効率化」が鍛えられる
算数や数学の試験の点数を劇的に向上させることができる暗算の力ですが、残念ながらこれは魔法の力ではありません。
また、天賦の才能でもありません。
暗算の力は、訓練によってしか身につけることができません。
例えば、そろばんを習うと、頭のなかにそろばんのイメージを持てるようになります。
計算問題をその「脳内そろばん」で計算すれば、短時間で答えを出すことができます。
しかしそのためには、そろばんを何十時間も弾かなければなりません。
また、数学の知識が増えていくと、「数式を変更する」テクニックを身につけることができます。
「68×54」を暗算で解くことは簡単ではありません。
しかしこの数式を、次のように変更すると、次第に暗算できるようになるでしょう。
68×(50+4)=
68×50+68×4=
34×2×50+(50+18)×4=
34×100+50×4+18×4=3400+200+72=3672
この「数式の変更」のポイントは「2×50」と「34×100」と「50×4」です。
この計算ならすぐに「100」「3400」「200」を出すことができます。
「×50」や「×100」を多くつくっていくことで、暗算ができるようになります。
また「インド式」の計算方法も、暗算の力を高めます。
「68×54」をインド式で計算すると、このようになります。
| 6(a) | 8(b) |
| 5(c) | 4(d) |
【a×c】×10×10 6×5(×10×10)=3000 |
| 【b×d】 8×4=32 |
【a×d+b×c】×10 [(6×4)+(8×5)]×10=640 | ||
日本式に慣れているとインド式は面倒に感じるかもしれません。
しかし、日本式は暗算に進化させることは難しいのですが、インド式なら「単純な計算の集まり」なので暗算に向いています。
ただしインド式を体得するにも、相当な計算練習が必要になります。
このように、暗算の力を身につけるには、相当な訓練が必要になります。
その訓練を乗り越えるには「最短距離で正解に到着したい」という気持ちと、「計算をとにかく効率化させたい」という気持ちが必要になります。
この2つの「したい」気持ちを持って暗算の訓練に取り組み、見事、暗算のスキルが身についたら、算数・数学の問題が簡単に思えます。
それは快感になります。
この経験と快感が、他教科でも活きてきます。
英単語の暗記訓練に集中的に取り組むと、急に、英語の問題が簡単に感じることができます。
元素の周期表の記訓練に集中的に取り組むと、急に化学式が見えてきます。
暗算の訓練は、「他の教科の訓練の練習」になるわけです。
だから暗算のスキルを身につけた子供は、他教科の成績もグングンの向上していくわけです。
計算では「粘り強く考える学習態度」が身につき「根気」が養われる
数学の学習レベルが上がると、複雑な計算はもう、暗算のように「あるスキルを身につけたら、あとは自動的に答えが出てくる」という方法では解けなくなります。
数学の複雑な計算を解くには、思考力が必要になります。
考えに考え抜いて、ようやく答えが出ます。
 計算は登山のようなものです。
計算は登山のようなものです。
登山をするとき山頂が見えているように、数学の問題には必ず答えがあります。
しかし、山頂にも答えにも、簡単にはたどり着けません。
山頂に到達するためには、基礎体力が必要です。
しかし体力だけでは登ることができません。
スニーカーで登ったら、途中で足を怪我してしまうからです。
登山には登山靴が必要です。
また、途中でお腹が減ったら動けなくなってしまうので、弁当と水を持っていかなければなりません。
弁当と水を手に持っていては危険なので、リュックサックを持ちます。
途中で夜がやってくれば、テントと寝袋が必要になります。
複雑な計算を解くにも「基礎体力、登山靴、弁当、水、リュックサック、テント、寝袋」が必要です。
例えば高校の数学なら「方程式、不等式、集合、論理、二次関数、図形、微分法、積分法」などがあります。
これらをひとつ身につけるたびに、計算の力がパワーアップしていきます。
しかし、方程式ひとつ身につけるだけでも、相当考えさせられます。
計算の力を身につけることは、思考力を鍛えることに他なりません。
計算の力を身につけることで獲得した「粘り強く考える学習態度」と「根気」も、他の教科で活かすことができます。
英語の学力を上げるには、英単語をたくさん覚えるだけでは足りません。
英単語をたくさん覚えて「見えた」と思えた英語も、レベルが上がると英単語の知識だけでは太刀打ちできないからです。
それで英文法を覚えるわけです。
文型、関係代名詞、現在進行形、現在完了形などは、登山靴や弁当、水、リュックサックのようなものです。
それらがないと、英語の成績を高めることはできません。
英語の勉強もレベルが上がると簡単でなくなるので、計算で鍛えた「粘り強く考える学習態度」と「根気」が必要になってきます。
まとめ~早めに快感を体験しよう
暗算の訓練も計算の練習も、大変な作業です。
「苦しい」と思うでしょう。
苦しさが募ると、ギブアップしたくなり、「暗算しなくてもいいかな」という誘惑に駆られます。
その誘惑を克服するには、快感体験が有効です。
暗算の訓練に取り掛かる前に、自分の計算力を計測しておきましょう。
例えば、2桁×2桁の掛け算の問題を20問用意して、それを何分で解けるか計っておきます。
そして、暗算を2カ月訓練したら、同じ問題を解いて時間を計ります。
驚異的に計算スピードが上がっていることがわかるでしょう。
これが快感体験です。
「苦しいけど必ず報われる」という気持ちがないと、訓練や練習を継続することはできません。
快感体験をすれば、「苦しいけど必ず報われる」ことが事実であることを知ることができます。
この記事を監修した人

「大成会」代表
池端 祐次
2013年「合同会社大成会」を設立し、代表を務める。学習塾の運営、教育コンサルティングを主な事業内容とし、札幌市区のチーム個別指導塾「大成会」を運営する。「完璧にできなくても、ただ成りたいものに成れるだけの勉強はできて欲しい。」をモットーに、これまで数多くの生徒さんを志望校の合格へと導いてきた。















